I was recently reading about how Cassandra uses a Bloom filter to check if any of its SSTables are likely to contain a given partition key or not without having to read the entire SSTable. This got me thinking about how I could implement a Bloom filter in Ruby.

Wait… what even is a Bloom filter?

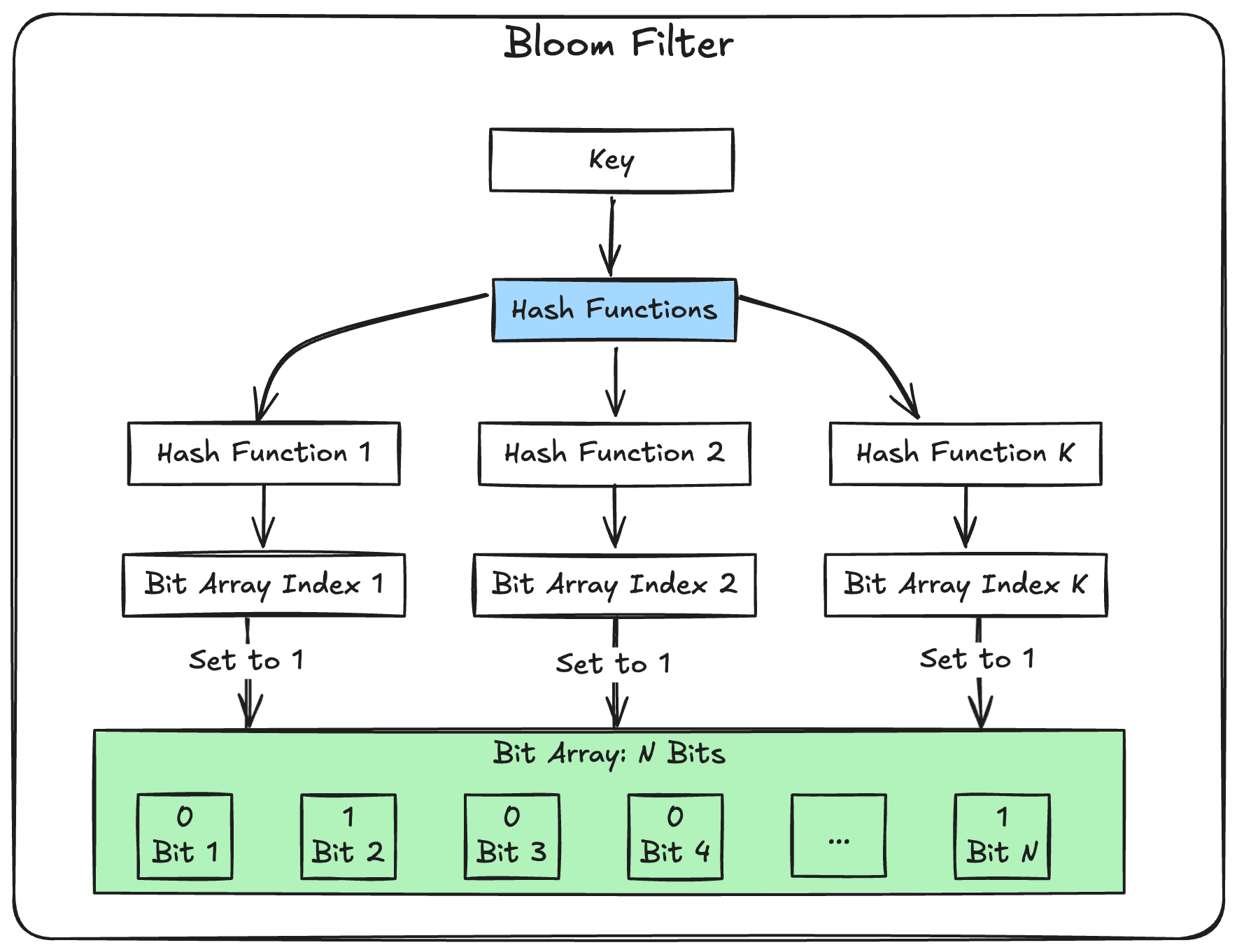
A Bloom filter is a space-efficient probabilistic data structure that is used to test whether an element is a member of a set. It can yield false positives, but not false negatives. This means that if the filter says an element is in the set, it might be, but if it says it’s not, then it definitely isn’t.

Bloom filters are often used in applications where false positives are acceptable but false negatives are not.

For example, if you are building a web crawler, you might want to use a Bloom filter to keep track of which URLs you’ve already visited. If the filter says a URL has been visited, you can skip it. If it says it hasn’t, you can go ahead and visit it. The cost of a false positive (visiting a URL that has already been visited) is much lower than the cost of a false negative (missing a URL that hasn’t been visited yet).

Okay, but how does this thing work?

A Bloom filter uses multiple hash functions to map elements to a bit array. When you add an element to the filter, it is hashed by each of the hash functions, and the corresponding bits in the array are set to 1.

To check if an element is in the filter (a.k.a membership check), it is hashed again, and if all the corresponding bits are set to 1, then the element is probably in the set. If any of the bits are 0, then the element is definitely not in the set.

Bloom Filter
Bloom Filter

Tuning the size and the number of hash functions

There’s some wild math behind choosing the right bit array size and the number of hash functions — I read it twice and still just nodded politely 😅.

The general rule of thumb is:

Let’s build one in Ruby!

Let’s start by creating a simple Ruby class for our Bloom filter and use a bit array to store our bits and a few hash functions to hash our items.

    class BloomFilter
  def initialize(size: 1000, hash_count: 3)
    @size = size
    @hash_count = hash_count
    
    # Initialize bit array with zeros
    @bit_array = Array.new(@size, false)
    @item_count = 0
  end

We will come back to the optimal size of the bit array and the number of hash functions later, but for now, let’s just use a default of 1000 bits and 3 hash functions.

Adding and checking items

The add method hashes the item and sets the corresponding bits in the bit array to true. The include? method checks if all the bits for the given item are set to true.

    require 'murmurhash3'

class BloomFilter
  ...

  def add(item)
    bit_positions(item).each do |position|
      @bit_array[position] = true
    end
    @item_count += 1
    self
  end

  def include?(item)
    bit_positions(item).all? { |position| @bit_array[position] }
  end

  private

  def bit_positions(item)
    item_str = item.to_s
    positions = []
    
    # Use different seeds to generate two independent hash values
    hash1 = MurmurHash3::V32.str_hash(item_str, 42)
    hash2 = MurmurHash3::V32.str_hash(item_str, 101)
    
    # Use double hashing technique to generate k hash functions
    # This is more efficient than computing k independent hashes
    @hash_count.times do |i|
      # h_i(x) = (hash1(x) + i * hash2(x)) % m
      position = (hash1 + i * hash2) % @size
      positions << position
    end
    
    positions
  end

I’m using the murmurhash3-ruby gem to create our hash functions based on the MurmurHash3 algorithm.

MurmurHash3 is a great hash function for Bloom filters. It’s non-cryptographic (so it’s fast!), produces uniformly distributed hash values, and supports seeding - which allows us to generate multiple different hash functions from a single algorithm.

Nothing fancy here, except for the fact that we are using double hashing to generate multiple hash functions from two independent hash values. This is more efficient than computing k independent hashes, even though it is a bit less intuitive and there is a bit of math behind it 😅.

All good so far?

Making it more efficient

Remember that wild math part I mentioned earlier? That’s where the formulas for calculating the optimal bit array size and number of hash functions come into play, based on the expected number of items and the desired false positive rate.

The formula for the optimal size of the bit array is:

    m = -(n * ln(p)) / (ln(2)^2)

Where:

The formula for the optimal number of hash functions is:

    k = (m / n) * ln(2)

Where:

    class BloomFilter
  attr_reader :size, :hash_count, :capacity, :false_positive_probability

  def initialize(capacity: 1000, false_positive_probability: 0.01)
    @capacity = capacity
    @false_positive_probability = false_positive_probability
    
    @size = calculate_size(capacity, false_positive_probability)
    @hash_count = calculate_hash_count(capacity, @size)

    @bit_array = Array.new(@size, false)
    @item_count = 0
  end

  private

  ...

  def calculate_size(capacity, fp_prob)
    # m = -n*ln(p)/(ln(2)^2)
    (-capacity * Math.log(fp_prob) / (Math.log(2)**2)).ceil
  end

  def calculate_hash_count(capacity, size)
    # k = (m/n)*ln(2)
    ((size.to_f / capacity) * Math.log(2)).ceil
  end
end

Great! We now have a working Bloom filter.

Time to try it out!

Let’s give our Bloom filter a quick test. Remember: it may say something is in the set when it’s not (a false positive), but never the other way around.

    filter = BloomFilter.new(capacity: 50, false_positive_probability: 0.01)

puts "Adding elements to the bloom filter..."
(0..100).each do |i|
  filter.add("item_#{i}")
end

puts "Checking for elements in the bloom filter..."
(0..100).each do |i|
  puts "item_#{i}: #{filter.include?("item_#{i}")}" # true
end

puts "Checking for non-existent elements..."
(101..200).each do |i|
  puts "item_#{i}: #{filter.include?("item_#{i}")}" # false (unless false positive)
end

The full source code is available in this repository.

Conclusion

Not every data structure has to be perfect, sometimes “probably in the set” is good enough. Bloom filters are a great example of smart trade-offs: they give us blazing-fast, memory-efficient membership checks where false positives are totally worth it.